Introduction

Hello. I have recently been spending a lot of time dithering. In image processing, dithering is the act of applying intentional perturbations or noise in order to compensate for the information lost during colour reduction, also known as quantisation. In particular, I’ve become very interested in a specific type of dithering and its application to colour palettes of arbitrary or irregular colour distributions. Before going into detail however, let’s briefly review the basics of image dithering.

Dithering in its simplest form can be understood by observing what happens when we quantise an image with and without modifying the source by random perturbation. In the examples below, a gradient of 256 grey levels is quantised to just black and white. Note how the dithered gradient is able to simulate a smooth transition from start to end.

An example of dithering using random noise. Top to bottom: original gradient, quantised after dithering, quantised without dithering.

While this is immediately effective, the random perturbations introduce a disturbing texture that can obfuscate details in the original image. To counter this, we can make some smart choices on where and by how much to perturb our input image in an attempt to add some structure to our dither and preserve some of the lost detail.

Ordered Dithering

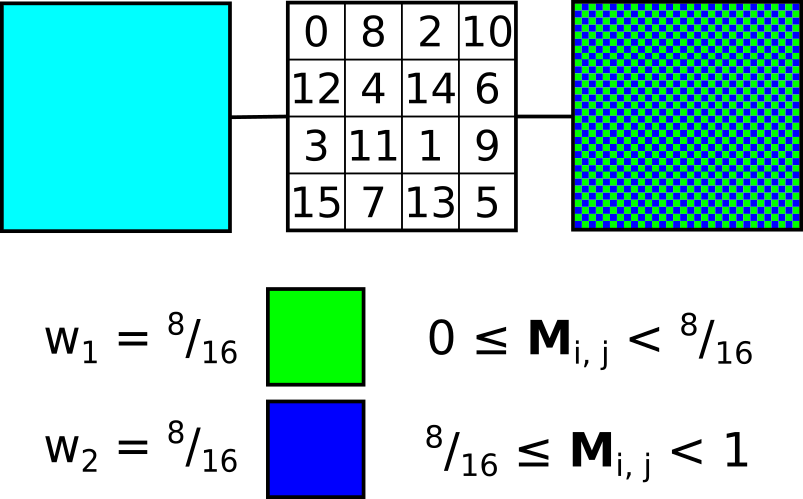
Instead of perturbing each pixel in the input image at random, we can choose to dither by a predetermined amount depending on the pixel’s position in the image. This can be achieved using a threshold map; a small, fixed-size matrix $\textbf{M}$ where each entry tells us the amount by which to perturb the input value $p$ , producing the dithered value $p'$ . This matrix is tiled across the input image and sampled for every pixel during the dithering process. The following describes a dithering function for a 4×4 matrix given the pixel raster coordinates $(x, y)$ :

$p^{\prime} = p + \textbf{M}_{i, j} - 0.5 \quad \text{where} \quad \textbf{M} = \dfrac{1}{16} \small{\begin{bmatrix} 0 & 8 & 2 & 10\\ 12 & 4 & 14 & 6\\ 3 & 11 & 1 & 9\\ 15 & 7 & 13 & 5 \end{bmatrix}}$

$\text{and} \quad (i, j) = (x \mod{4}, y \mod{4})$

Comparison between random dithering and ordered dithering. Left to right: random, ordered.

We can see that the threshold map distributes perturbations more optimally than purely random noise, resulting in a clearer and more detailed final image. The algorithm itself is extremely simple and trivially parallelisable, requiring only a few operations per pixel.

Error-Diffusion Dithering

Another way to approach dithering is to analyse the input image in order to make informed decisions about how best to perturb pixel values prior to quantisation. Error-diffusion dithering does this by sequentially taking the quantisation error for the current pixel (the difference between the input value and the quantised value) and distributing it to surrounding pixels in variable proportions according to a diffusion kernel $\textbf{K}$ . The result is that input pixel values are perturbed just enough to compensate for the error introduced by previous pixels.

$\textbf{K} = \dfrac{1}{16} \large{\begin{bmatrix} 0 & \# & 7 \\ 3 & 5 & 1 \end{bmatrix}} \quad \text{centered on} \enspace p \enspace \text{at} \enspace \#$

Comparison between error-diffusion dithering and ordered dithering. Left to right: error-diffusion, ordered.

Due to this more measured approach, error-diffusion dithering is even better at preserving details and can produce a more organic looking final image. However, the algorithm itself is inherently serial and not easily parallelised. Additionally, the propagation of error can cause small discrepancies in one part of the image to cascade into other distant areas. This is very obvious during animation, where pixels will appear to jitter between frames. It also makes files harder to compress.

An animated sequence quantised using error-diffusion dithering. Note the jittering artifacts present in the background.

Palette Quantisation

Moving beyond just black and white towards full-colour variable palettes presents another set of problems. Taking the methods presented above and quantising an image using an arbitrary colour palette reveals that error-diffusion is also better at preserving colour information when compared to ordered dithering.

Comparison of error-diffusion vs ordered dithering using an 8-colour irregular palette. Left to right: original image, error-diffusion, ordered.

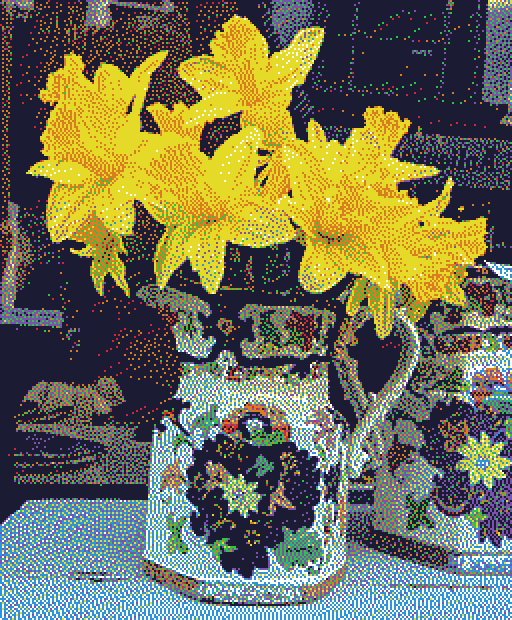
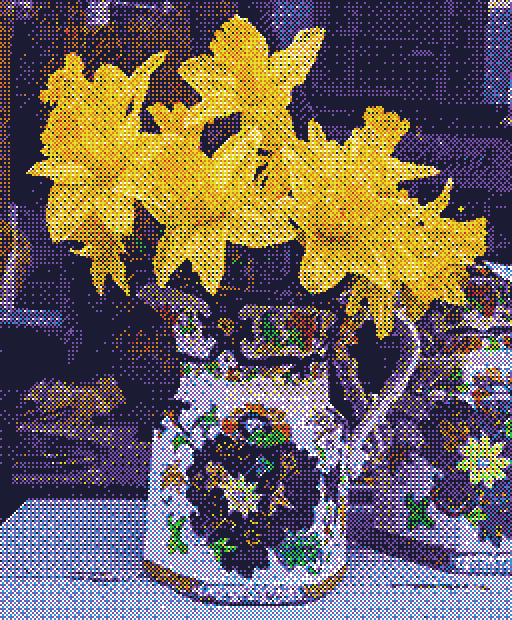
Intuitively, it’s not too difficult to understand why this is the case. Remember that error-diffusion works in response to the relationship between the input value and the quantised value. In other words, the colour palette is already factored in during the dithering process. On the other hand, ordered dithering is completely agnostic to the colour palette being used. Images are perturbed the same way every time, regardless of the given palette.

Regular vs Irregular Palettes

Under certain circumstances, it’s possible to modify ordered dithering so that it can better handle colour information. This requires that we use a palette that is regularly distributed in colour space. A regular palette is composed of all possible combinations of red, green and blue tristimulus values, where each colour component is partitioned into a number of equally spaced levels. For example, 6 levels of red, green and blue totals 6³ = 216 unique colours, equivalent to the common web-safe palette.

Visual representation of an RGB colour cube that has been equally divided into 216 coloured boxes (6 levels along each axis).

This time, before we perturb the input image, we take the value given by the threshold matrix and divide it by $L$ , where $L$ is the number of levels for each colour component. As a result, each pixel is perturbed just enough to cover the minimal distance between two colours in the palette. Since the entire palette is evenly distributed across colour space, we only need to modify the range of perturbation along each axis. The dithering equation then becomes:

$p^{\prime} = p + \frac{1}{L} (\textbf{M}_{i, j} - 0.5)$

The whole algorithm can be expressed in psuedocode like so:

for each pixel in image
   let value = value in threshold matrix at (x, y)
   let offset = pixel + (value - 0.5) * (1.0 / number of levels)
   set pixel as closest colour to offset

Comparison between error-diffusion and ordered dithering using an 8-colour regular palette. Left to right: error-diffusion, ordered.

By appropriately scaling the perturbation amount for each colour channel separately, we can also extend this to work with palettes where $L$ is different for each colour component, provided that they are still regularly spaced. Unfortunately, the less regular the palette is, the less effective this technique becomes. If we wish to leverage the strengths of ordered dithering for use with irregular or arbitrary palettes, a more general solution is needed.

The Probability Matrix

Another way to look at our threshold matrix is as a kind of probability matrix. Instead of offsetting the input pixel by the value given in the threshold matrix, we can instead use the value to sample from the cumulative probability of $N$ possible candidate colours, where each colour $c_n$ is assigned a probability or weight $w_n$ . Each colour’s weight represents it’s proportional contribution to the input colour. Colours with greater weight are then more likely to be picked for a given pixel and vice-versa, such that the local average for a given region should converge to that of the original input value. We can call this the N-candidate approach to palette dithering.

$p^{\prime} = \begin{cases} c_1, & 0 \le \textbf{M}_{i, j} < t_1 \\ c_2, & t_1 \le \textbf{M}_{i, j} < t_2 \\ \dots \\ c_N, & t_{N-1} \le \textbf{M}_{i, j} < t_{N} \end{cases}$

$\quad \text{where} \quad \displaystyle t_k = \sum_{i = 1}^{k} w_i$

A simple demonstration of the use of a probability matrix to select from two candidate colours. In this case, both colours contribute equally to the initial input colour. The normalised threshold matrix value at $\textbf{M}_{i, j}$ for a given pixel is compared against the cumulative probability of each candidate.

A simple demonstration of the use of a probability matrix to select from two candidate colours. In this case, both colours contribute equally to the initial input colour. The normalised threshold matrix value at $\textbf{M}_{i, j}$ for a given pixel is compared against the cumulative probability of each candidate.

This approach shares a lot in common with the idea of multivariate interpolation over scattered data. Multivariate interpolation attempts to estimate values at unknown points within an existing data set and is often used in fields such as geostatistics or for geophysical analysis like elevation modelling. We can think of our colour palette as the set of variables we want to interpolate from, and our input colour as the unknown we’re trying to estimate. We can borrow some ideas from multivariate interpolation to develop more effective dithering algorithms.

N-Closest Algorithm

The N-closest or N-best dithering algorithm is a straightforward solution to the N-candidate problem. As the name suggests, the set of candidates is given by the $N$ closest palette colours to the input pixel. To determine their weights, we simply take the inverse of the distance to the input pixel. This is essentially the inverse distance weighting (IDW) method for multivariate interpolation, also known as Shepard’s method. The following pseudocode sketches out a possible implementation:

for each pixel in image
   let sum of weights = 0.0
   let list of candidates = N closest colours to pixel
   for each candidate in list of candidates
      candidate.weight = 1.0 / distance to candidate
      sum of weights += candidate.weight
   for each candidate in list of candidates
      candidate.weight /= sum of weights
   let seed = value in threshold matrix at (x, y)
   let sum = 0.0
   for each candidate in list of candidates
      sum += candidate.weight
      if seed < sum
         set pixel as candidate 
         process next pixel

One by-product of weighing the candidates by their distance is that the resulting output image is prone to false contours or banding. Increasing $N$ reduces this effect at the cost of added granularity or high frequency noise due to the introduction of ever more distant colours to the set. I recommend taking a look at the original paper if you’re interested in learning a bit more about the algorithm^[1].

Comparison of N-closest dithering using an 8-colour irregular palette. Left to right: $N = 2, N = 4, N = 8$ .

Note that IDW often includes a variable exponent $s$ that is applied to the distance before taking the inverse. For a given distance $d$ , the weight $w$ of the candidate becomes:

$w = \dfrac{1}{d^s}$

As you might expect, the result of this is that colours which lie closer to the input pixel are given a greater proportion of the total influence with ever-increasing values of $s$ . This is not mentioned in the cited paper but it might be nice to consider for your own implementation.

N-Convex Algorithm

Instead of taking the $N$ nearest candidates to $p$ , we can look for a set of $N$ candidates whose centroid is close to $p$ . The N-convex algorithm works by finding the closest colour to a given target colour for $N$ iterations, where the target is first initialised to be equal to the input pixel. Every iteration the closest colour added to the candidate list, and the quantisation error between it and the original input pixel is added to the target.

for each pixel in image
   let goal = pixel
   do n times
      candidate[n] = closest colour to goal
      mark candidate[n] as used
      goal += pixel - candidate[n]

If this sounds familiar to you, it’s because this method works very similarly to error-diffusion. Instead of letting adjacent pixels compensate for the error, we’re letting each successive candidate compensate for the combined error of all previous candidates.

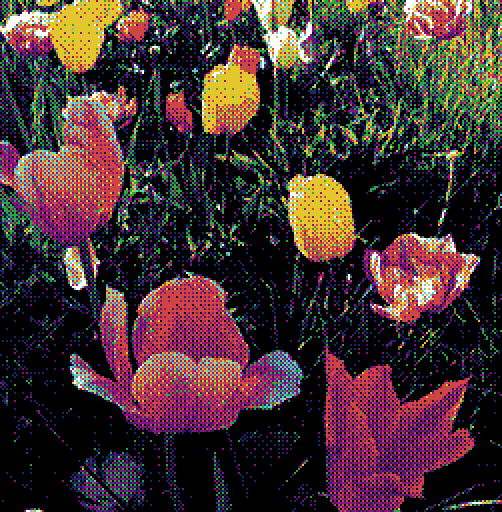
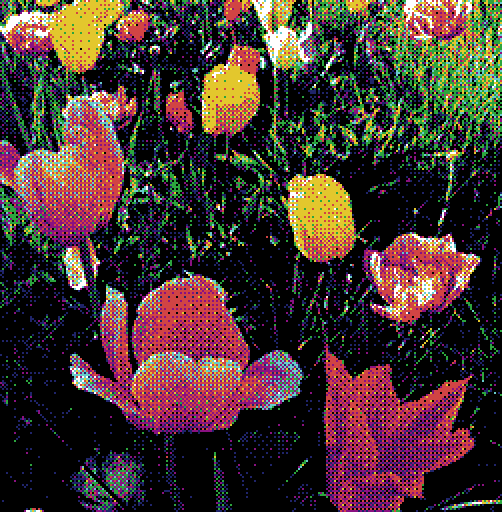
Comparison of the N-closest and N-convex algorithms using an 8-colour irregular palette with $N = 4$ . Left to right: N-closest, N-convex.

Like the N-closest algorithm, the weight of each candidate is given by the inverse of its distance to the input colour. Because of this, both algorithms produce output of a similar quality, although the N-convex method is measurably faster. As with the last algorithm, more details can be found in the original paper^[2].

The Linear Combination

If we think about this algebraically, what we really want to do is express the input pixel $p$ as the weighted sum of palette colours. This is nothing more than a linear combination of palette colours $c_n$ with weights $w_n$ :

$p = \displaystyle \sum_{n = 1}^{N} c_n w_n \quad \text{where} \quad w_n \ge 0$

Note however that depending on $N$ as well as the distribution of colours in the palette, there may not always be an exact solution for any given $p$ . Instead we’ll say that we want to minimise the absolute error between $p$ and some linear combination $p^{\prime}$ , or $|p^{\prime} - p|$ .

As it stands, inverse distance weighting is not very good at minimising this error. Another approach is needed if we want to improve the image quality.

Thomas Knoll’s Algorithm

Like the N-convex algorithm, this algorithm attempts to find a set of candidates whose centroid is close to $p$ . The key difference is that instead of taking $N$ unique candidates, we allow candidates to populate the set multiple times. The result is that the weight of each candidate is simply given by its frequency in the list, which we can then index by random selection:

for each pixel in image
   let goal = pixel
   do n times
      candidate[n] = closest colour to goal
      goal += pixel - candidate[n]
   let seed = random integer from 0 to n
   set pixel as candidate[seed]

This algorithm attempts to minimise $|p^{\prime} - p|$ numerically. Because of this, the quality of the dither produced by Knoll’s algorithm is much higher than any other of the N-candidate methods we have covered so far. It is also the slowest however, as it requires a greater $N$ per-pixel to be really effective. More details are given in Knoll’s now expired patent^[3]. I have put together a GPU implementation of Knoll’s algorithm on Shadertoy here.

Comparison between Thomas Knoll’s algorithm and the N-convex algorithm, using an 8-colour irregular palette. Left to right: original image, Knoll, N-convex ( $N = 4$ ).

Barycentric Coordinates

Another way to approach the linear combination is to look at it geometrically. This is where the idea of barycentric coordinates can help. A barycentric coordinate system describes the location of a point as the weighted sum of the regular coordinates of the vertices forming a simplex. In other words, it describes a linear combination with respect to a set of $N$ points, where $N \le D + 1$ in $D$ -dimensional space.

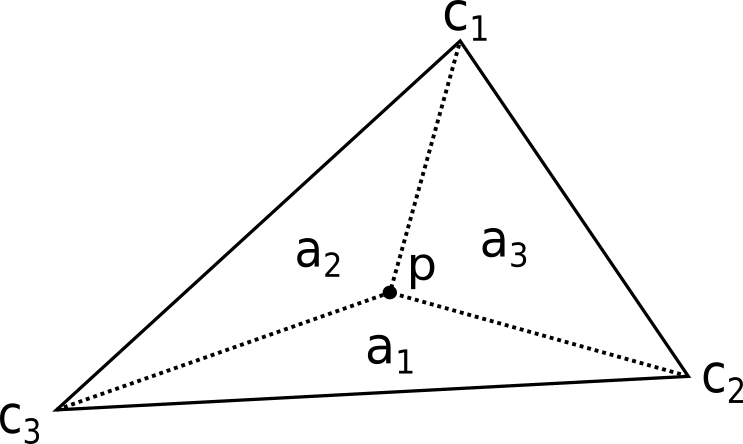
The weight of each term is given by the proportion of each sub-triangle area $a_1, a_2, a_3$ with respect to the total triangle area $A$ . Algebraically, this can be expressed like so:

$p = \dfrac{a_1}{A}c_1 + \dfrac{a_2}{A}c_2 + \dfrac{a_3}{A}c_3$

Knowing this, we can modify the N-Convex algorithm covered earlier such that the candidate weights are given by the barycentric coordinates of the input pixel after being projected onto a triangle whose vertices are given by three surrounding colours, abandoning the IDW method altogether¹. This results in a fast and exact minimisation of $|p' - p|$ , with the final dither being closer in quality to that of Knoll’s Algorithm.

Comparison between barycentric (triangular) dithering and Knoll’s algorithm using an 8-colour irregular palette. Left to right: barycentric, Knoll.

Triangulated Irregular Network

Recall that a barycentric coordinate system is given with respect to a $D$ -dimensional simplex, where $D$ is no larger than the dimensional space. Given a set of scattered points, it’s possible to create a tessellation of the space by forming simplices from the points, such that any input point that lies within the convex hull of the scattered set can be expressed in terms of the enclosing simplex and its corresponding barycentric coordinates². This can be understood as a kind of triangulated irregular network (TIN).

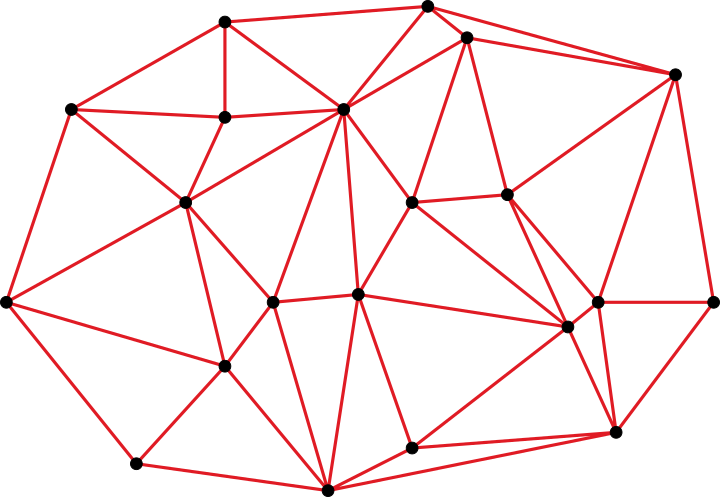
While there exist many possible ways to triangulate a set of points, the most common method for TINs is the Delaunay triangulation. This is because Delaunay triangulations tend to produce more regular tessellations that are better suited to interpolation. In theory, we can represent our colour palette as a TIN by computing the 3D Delaunay triangulation of the colours in colour space. The nice thing about this is that it makes finding an enclosing simplex much faster; the candidate selection process is simply a matter of determining the enclosing tetrahedron of an input point within the network using a walking algorithm, and taking the barycentric coordinates as the weights.

Comparison between the TIN, Knoll’s algorithm, and N-convex dithering using an 8-colour irregular palette. Left to right: TIN, Knoll, N-convex (N=4).

If executed well, Delaunay-based tetrahedral dithering can outperform the N-convex method and produce results that rival Knoll’s algorithm. The devil is in the detail however, as actually implementing a robust Delaunay triangulator is a non-trivial task, especially where numerical stability is concerned. The additional memory overhead required by the triangulation structure may also be a concern.

Natural Neighbour Interpolation

We’ve looked at how we can geometrically find the linear combination using barycentric coordinates, but it is not the only way to do so. Natural neighbour interpolation works by observing what happens when an input point is inserted into a set of points represented by a Voronoi diagram. The Voronoi diagram is simply a partition of space into polygonal regions for each data point, such that any point inside a given region is proximal to its corresponding data point.

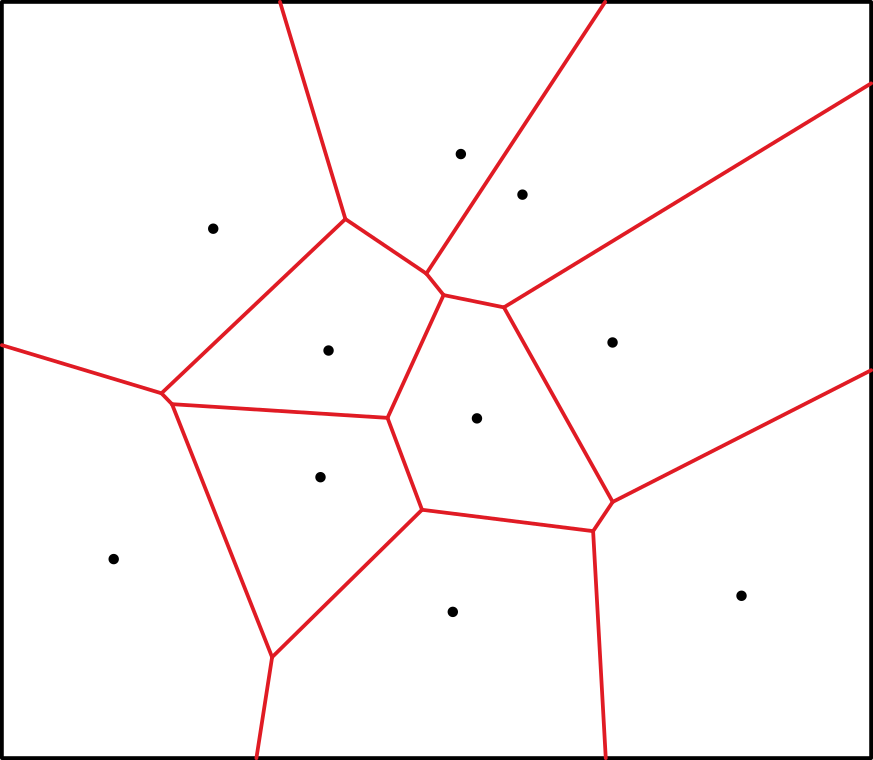
Any point within a given Voronoi region is proximal to the data site (black point) associated with that region.

When another data point is inserted and the Voronoi diagram reconstructed, the newly created region displaces the area that once belonged to the old regions. Those points whose regions were displaced are considered natural neighbours to the new point. The weight of each natural neighbour is given by the area $a_n$ taken from the total area $A$ occupied by the new region. In 3D, we measure polyhedral volumes instead of areas.

$p = \displaystyle \sum_{n = 1}^{N} c_n w_n \quad \text{where} \quad w_n = \dfrac{a_n}{A}$

The query point $p$ creates a new Voronoi region shown in blue, displacing some of the old regions. The weight of each natural neighbour $c_n$ is derived from the area of the displaced region $a_n$ .

Natural neighbour interpolation has a number of strengths over linear barycentric interpolation. Namely, it provides a smooth or continuous slope between samples³, and is always the same for a given point set, unlike the TIN where the quality of the triangulation can produce biases in the outcome, even in the best case.

Comparison between TIN and natural neighbour dithering, using a 16-colour irregular palette. Left to right: TIN, Natural Neighbour.

Implementing natural neighbour interpolation implies the construction of a geometric Voronoi diagram, however this is not strictly the case. Since the Delaunay triangulation is the dual graph of the Voronoi diagram, all the information needed to perform natural neighbour interpolation is already implicit within the triangulation itself. Algorithms to determine natural neighbours from the Delaunay triangulation can be found in several papers within the literature^[4][5]. Unfortunately the relative complexity of natural neighbour interpolation means that it is slower than barycentric interpolation by a considerable margin.

Joel Yliluoma’s Algorithms

A notable resource on the topic of ordered dithering using arbitrary palettes is Joel Yliluoma’s Arbitrary-Palette Positional Dithering Algorithm. One key difference of Yliluoma’s approach is in the use of error metrics beyond the minimisation of $|p^{\prime} - p|$ . Yliluoma notes that the perceptual or psychovisual quality of the dither must be taken into account in addition to its mathematical accuracy. This is determined by use of some cost function which considers the relationship between a set of candidate colours. The number of candidates, the particular cost function, and the thoroughness of the selection process itself give rise to a number of possible implementations, each offering varying degrees of quality and time complexity.

Comparison between Knoll’s and Yliluoma’s algorithms using a 16-colour irregular palette. Left to right: Knoll, Yliluoma. The ‘*Yliluoma’s ordered dithering algorithm 2*‘ variant was used.

Yliluoma’s algorithms can produce very good results, with some variants matching or even exceeding that of Knoll’s. They are generally slower however, except in a few cases.

Tetrapal: A Palette Triangulator

Most of the algorithms described here are quite straightforward to implement. Some of them can be written in just a few lines of code, and those that require a bit more effort can be better understood by reading through the relevant papers and links I have provided. The exception to this are those that rely on the Delaunay triangulation to work. Robust Delaunay triangulations in 3D are fairly complex and there isn’t any publicly available software that I’m aware of that leverages them for dithering in the way I’ve described.

To this end, I have written a small C library for the sole purpose of generating the Delaunay triangulation of a colour palette and using the resulting structure to perform barycentric interpolation as well as natural neighbour interpolation for use in colour image dithering. The library and source code is available for free on Github. I’ve included an additional write up that goes into a bit more detail on the implementation and also provides some performance and quality comparisons against other algorithms. Support would be greatly appreciated!

Appendix I: Candidate Sorting

When using the probability matrix to pick from the candidate set, it is important that the candidate array be sorted in advance. Not doing so will fail to preserve the patterns distinctive of ordered dithering. A good approach is to sort the candidate colours by luminance, or the measure of a colour’s lightness⁴. When this is done, we effectively minimise the contrast between successive candidates in the array, making it easier to observe the pattern embedded the matrix.

Comparison between an unsorted and a luminance sorted candidate set, using Knoll’s algorithm on an 8-colour irregular palette. Left to right: unsorted, sorted.

If the number of candidates for each pixel grows too large (as is common in algorithms such as Knoll and Yliluoma) then sorting the candidate list for every pixel can have a significant impact on performance. A solution is to instead sort the palette in advance and keep a separate tally of weights for every palette colour. The weights can then be accumulated by iterating linearly through the tally of sorted colours.

sort palette by luminance
let weights[palette size] = weight for each colour
...
for i in range 0 to palette size - 1
   cumulative weight += weights[i]
   if cumulative weight < probability value
      set pixel as palette[i]

Appendix II: Linear RGB Space

Most digital images intended for viewing are generally assumed to be in sRGB colour space, which is gamma-encoded. This means that a linear increase of value in colour space does not correspond to a linear increase in actual physical light intensity, instead following more of a curve. If we want to mathematically operate on colour values in a physically accurate way, we must first convert them to linear space by applying gamma decompression. After processing, gamma compression should be reapplied before display. The following C code demonstrates how to do so following the sRGB standard:

void srgb_to_linear(float pixel[3])
{
	pixel[0] = pixel[0] > 0.04045f ? powf((pixel[0] + 0.055f) / 1.055f, 2.4f) : pixel[0] / 12.92f;
	pixel[1] = pixel[1] > 0.04045f ? powf((pixel[1] + 0.055f) / 1.055f, 2.4f) : pixel[1] / 12.92f;
	pixel[2] = pixel[2] > 0.04045f ? powf((pixel[2] + 0.055f) / 1.055f, 2.4f) : pixel[2] / 12.92f;
}

void linear_to_srgb(float pixel[3])
{
	pixel[0] = pixel[0] > 0.0031308f ? 1.055f * powf(pixel[0], 1.0f / 2.4f) - 0.055f : 12.92f * pixel[0];
	pixel[1] = pixel[1] > 0.0031308f ? 1.055f * powf(pixel[1], 1.0f / 2.4f) - 0.055f : 12.92f * pixel[1];
	pixel[2] = pixel[2] > 0.0031308f ? 1.055f * powf(pixel[2], 1.0f / 2.4f) - 0.055f : 12.92f * pixel[2];
}

Comparison between error-diffusion dithering in sRGB space and linear RGB space. Left to right: sRGB, linear.

Appendix III: Threshold Matrices and Noise Functions

All of the examples demonstrating ordered dithering so far have been produced using a specific type of threshold matrix commonly known as a Bayer matrix. In theory however any matrix could be used and a number of alternatives are available depending on your qualitative preference. Matrices also don’t have to be square or even rectangular; polyomino-based dithering matrices have been explored as well^[6].

The classic Bayer or ‘dispersed-dot’ pattern arranges threshold values in an attempt to optimise information transfer and minimise noise^[7]. The matrix dimensions are typically a power of two. The following values describe an 8×8 matrix:

int bayer_matrix[8][8] = { 
{  0, 32, 8, 40, 2, 34, 10, 42 },
{ 48, 16, 56, 24, 50, 18, 58, 26 },
{ 12, 44, 4, 36, 14, 46, 6, 38 },
{ 60, 28, 52, 20, 62, 30, 54, 22 },
{  3, 35, 11, 43, 1, 33, 9, 41 },
{ 51, 19, 59, 27, 49, 17, 57, 25 },
{ 15, 47, 7, 39, 13, 45, 5, 37 },
{ 63, 31, 55, 23, 61, 29, 53, 21 } };

The halftone or ‘clustered-dot’ matrix uses a dot pattern reminiscent of traditional photographic halftoning. Here a diagonal variant of the pattern is given:

int halftone_matrix[8][8] = {
{ 24, 10, 12, 26, 35, 47, 49, 37 },
{ 8, 0, 2, 14, 45, 59, 61, 51 },
{ 22, 6, 4, 16, 43, 57, 63, 53 },
{ 30, 20, 18, 28, 33, 41, 55, 39 },
{ 34, 46, 48, 36, 25, 11, 13, 27 },
{ 44, 58, 60, 50, 9, 1, 3, 15 },
{ 42, 56, 62, 52, 23, 7, 5, 17 },
{ 32, 40, 54, 38, 31, 21, 19, 29 } };

The blue noise or ‘void-and-cluster’ dither pattern avoids directional artefacts while retaining the optimal qualities of the Bayer pattern. The Bayer matrix can in fact be derived from the void-and-cluster generation algorithm itself^[8].

You can access some tiled blue noise textures in plain text format here. I have also released a small C library for generating these textures.

It’s also possible to abandon the threshold matrix altogether and instead calculate a value for every pixel coordinate at runtime. If the function is simple enough this can be a good and efficient way to break up patterns and create interesting textures.

White noise simply uses a random number generator to produce threshold values.

float white_noise(int x, int y)
{
    return (float)rand() / RAND_MAX;
}

Interleaved gradient noise is a form of low-discrepancy sequence that attempts to distribute values more evenly across space when compared to pure white noise^[9].

float interleaved_gradient_noise(int x, int y)
{
    return fmodf(52.9829189f * fmodf(0.06711056f * (float)x + 0.00583715f * (float)y, 1.0f), 1.0f);
}

The R-sequence is another type of low-discrepancy sequence based on specially chosen irrational numbers^[10]. It is similar to interleaved gradient noise but is simpler to compute and possibly more effective as a dither, particularly when augmented with a triangle wave function as demonstrated:

float r_sequence(int x, int y)
{
    float value = fmodf(0.7548776662f * (float)x + 0.56984029f * (float)y, 1.0f);
	return value < 0.5f ? 2.0f * value : 2.0f - 2.0f * value;
}

Footnotes

¹ It’s also possible to use 4 candidates per pixel and compute the barycentric coordinates of the resulting tetrahedron, but using 3 candidates forming a triangle is more straightforward. ↑

² For points outside the convex hull, an acceptable solution is to find the closest point on the surface and determine the barycentric coordinates for that point instead. ↑

³ Strictly speaking, the slope is continuous everywhere except for the data points themselves. ↑

⁴ A good discussion on luminance and how to calculate it can be found on this stack exchange question. ↑

References

[1] K. Lemström, J. Tarhio & T. Takala: “Color Dithering with n-Best Algorithm” (1996). ↑

[2] K. Lemström & P. Fränti: “N-Candidate methods for location invariant dithering of color images” (2000). ↑

[3] T. Knoll: “Pattern Dithering” (1999). US Patent No. 6,606,166. ↑

[4] M. Sambridge, J. Braunl & H. McQueen: “Geophysical parametrization and interpolation of irregular data using natural neighbours” (1995). ↑

[5] L. Liang & D. Hale: “A stable and fast implementation of natural neighbour
interpolation” (2010). ↑

[6] D. Vanderhaeghe & V. Ostromoukhov: “Polyomino-Based Digital Halftoning” (2008). ↑

[7] B. E. Bayer: “An optimum method for two-level rendition of continuous-tone pictures” (1973). ↑

[8] R. Ulichney: “The void-and-cluster method for dither array generation” (1993). ↑

[9] J. Jimenez: “Next Generation Post Processing in Call of Duty: Advanced Warfare” (2014). ↑

[10] M. Roberts: “The Unreasonable Effectiveness of Quasirandom Sequences” (2018). ↑

Ordered Dithering with Arbitrary or Irregular Colour Palettes

Introduction

Ordered Dithering

Error-Diffusion Dithering

Palette Quantisation

Regular vs Irregular Palettes

The Probability Matrix

N-Closest Algorithm

N-Convex Algorithm

The Linear Combination

Thomas Knoll’s Algorithm

Barycentric Coordinates

Triangulated Irregular Network

Natural Neighbour Interpolation

Joel Yliluoma’s Algorithms

Tetrapal: A Palette Triangulator

Appendix I: Candidate Sorting

Appendix II: Linear RGB Space

Appendix III: Threshold Matrices and Noise Functions

Footnotes

References

Published by matejlou

Leave a Comment Cancel reply

Introduction

Ordered Dithering

Error-Diffusion Dithering

Palette Quantisation

Regular vs Irregular Palettes

The Probability Matrix

N-Closest Algorithm

N-Convex Algorithm

The Linear Combination

Thomas Knoll’s Algorithm

Barycentric Coordinates

Triangulated Irregular Network

Natural Neighbour Interpolation

Joel Yliluoma’s Algorithms

Tetrapal: A Palette Triangulator

Appendix I: Candidate Sorting

Appendix II: Linear RGB Space

Appendix III: Threshold Matrices and Noise Functions

Footnotes

References

Share this:

Related

Published by matejlou

Leave a Comment Cancel reply